Matematikk-seminar med Maple-demo
Ivar Skau og Harald Pleym
Mathematics possesses not only truth, but supreme beauty
- a beauty cold and au stere, like that of sculpture,
without appeal to any part of our weaker nature...
sublimely pure, and capable of a stern perfection
such as only the greatest art can show
Bertrand Russell
![[Maple Bitmap]](images/Innhold1.gif)
![[Maple OLE 2.0 Object]](images/Innhold2.gif)
- En rotasjon
- En speiling
- En translasjon (parallellforskyvning)
- En gliderefleksjon
Symmetri og ornamentikk
Symmetri
Det klassiske symmetribegrepet
En symmetriegenskap ved en figur består i at den er invariant ved en kongruenstransformasjon (en avstandsbevarende transformasjon). Eksempler: Speiling, rotasjon . Hva mere?:
Setning: Enhver kongruenstransformasjon i planet kan klassifiseres som
En endelig figurs symmetriegenskap er gitt ved
1)
Rotasjoner
, symmetrigruppene er
![]() , ...
, ...
Eksempel
på
![]() :
:
| > | alpha:=2*Pi/6: |
| > | Rotasjon(pltHP(red),alpha,5); |
![[Maple Plot]](images/Innhold5.gif)
| > | alpha:=67/180*Pi: |
| > | Rotasjon(pltHP(red),alpha,5); |
![[Maple Plot]](images/Innhold6.gif)
| > | R:=i->Rotasjon(pltHP(red),alpha,i): |
| > | display(seq(R(i),i=0..20),insequence=true); |
![[Maple Plot]](images/Innhold7.gif)
| > | Rotasjon(pltHP(red),alpha,90); |
![[Maple Plot]](images/Innhold8.gif)
2)
Speiling
, symmetrigruppene er
![]() , ...
, ...
Eksempel
på
![]() :
:
| > | L1:=[[0,0],[1,0]]: L2:=[[0,0],[1,tan(Pi/5)]]: |
| > | S:=Speiling(t1,L1,L2,axes=none,scaling=constrained):%; |
![[Maple Plot]](images/Innhold11.gif)
| > | rot:=u->rotate(p2,u): plt:=u->display(S,rot(u)): display(seq(plt(2*Pi/100*i),i=0..20),insequence=true,scaling=constrained); |
![[Maple Plot]](images/Innhold12.gif)
| > | beta:=72/180*Pi: |
| > | display(S,rotate(S,2*beta),rotate(S,3*beta),scaling=constrained); |
![[Maple Plot]](images/Innhold13.gif)
Båndmønster
| > | BåndMønster(1,red,8); |
| > | BåndMønster(2,blue,8); |
| > | BåndMønster(3,coral,8); |
| > | BåndMønster(4,cyan,8); |
| > | BåndMønster(5,magenta,10); |
| > | BåndMønster(6,maroon,10); |
| > | BåndMønster(7,pink,4); |
| > | BåndMønster(8,turquoise,8); |
![]()
![[Maple Plot]](images/Innhold15.gif)
![[Maple Plot]](images/Innhold16.gif)
![[Maple Plot]](images/Innhold17.gif)
![[Maple Plot]](images/Innhold18.gif)
![[Maple Plot]](images/Innhold19.gif)
![[Maple Plot]](images/Innhold20.gif)
FermatPunktet
| > | a,alpha,b,beta,d,e:=-1,0,1,0,0,-sqrt(3): |
| > | FermatPunktet(1,1,a,alpha,b,beta,d,e,XY,G); |
![[Maple Plot]](images/Innhold21.gif)
| > | XY; |
![]()
| > | G; |
![[Maple Plot]](images/Innhold23.gif)
| > | p:=(c,phi)->FermatPunktet(c,phi,a,alpha,b,beta,d,e,XY,G): |
| > | display(seq(p(cos(Pi/41*i),sin(Pi/41*i)),i=1..38),tickmarks=[4,4],insequence=true,scaling=constrained); |
![[Maple Plot]](images/Innhold24.gif)
Similariteter og logaritmiske spiraler
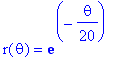
| > | plt:=n->polarplot(exp(-theta/20),theta=0..n*2*Pi,numpoints=1500,thickness=2,scaling=constrained): |
| > | plt(20); |
![[Maple Plot]](images/Innhold26.gif)
Rotasjon av en logaritmisk spiral
![[Maple Plot]](images/Innhold27.gif)
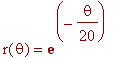
Rotasjon mot urviseren gir en ekspansjon, rotasjon med urviseren gir en kontraksjon
Spiralformet gangmønster
Fire innsekter jager hverandre på en kvadratisk flate. Hvert innsekt har hele tiden kurs mot naboen.
![[Maple Plot]](images/Innhold29.gif)
Kjeglespiral
| > | display(seq(Spiral(i),i=1..24),lightmodel=light2,insequence=true,orientation=[-71,66]); |
![[Maple Plot]](images/Innhold30.gif)
-
 : polar coordinates
: polar coordinates
-
 : tilt of ellipse major axis from horizontal plane
: tilt of ellipse major axis from horizontal plane
-
 : angle on each cross section
: angle on each cross section
-
 : angle between the plane of the cross section and the helical axis
: angle between the plane of the cross section and the helical axis
-
 : rotation of the elliptical cross section with respect to the horizonatl plane
: rotation of the elliptical cross section with respect to the horizonatl plane
-
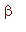 : angle between the helical axis (
: angle between the helical axis (
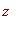 ) and local aperture line
) and local aperture line
- R: length of aperture generating curve (can itself be a function of parameters and s to have a nonuniform cross sections
- a: major semiaxis of the elliptical cross section
- b: minor semiaxis
-
D: sense of coiling
Kilde : Digital Seashells av M. B. Cortie , Comput. & Graphics Vol 17, No. 1 pp. 79-84, 1993
Sjøskjell
Punktet (
![]() ) på et skjell kan skrives på formen:
) på et skjell kan skrives på formen:
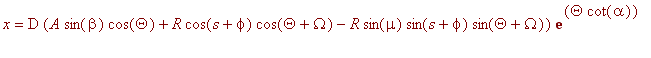
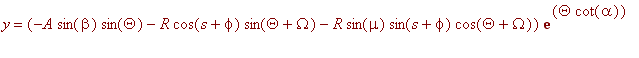
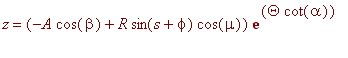
Parametrene er
Skjell
Natalina
![]()
| > | Ld1:=[80,40,55,10,30,25,12,16,0,0,0,0,0]: theta1:=[-4*Pi,4*Pi]: S:=[-270,62]: Grid:=[100,200]: SeaShell(Ld1,Grid,theta1,S,Natalina,scaling=constrained,orientation=[-68,80],style=patchnogrid,lightmodel=light2,shading=xy); |
![[Maple Plot]](images/Innhold43.gif)
Natalina i aksjon
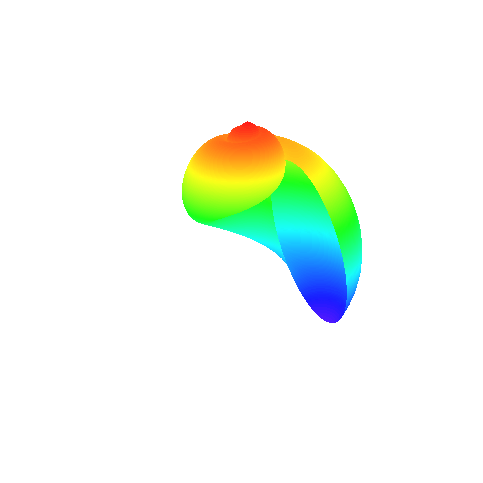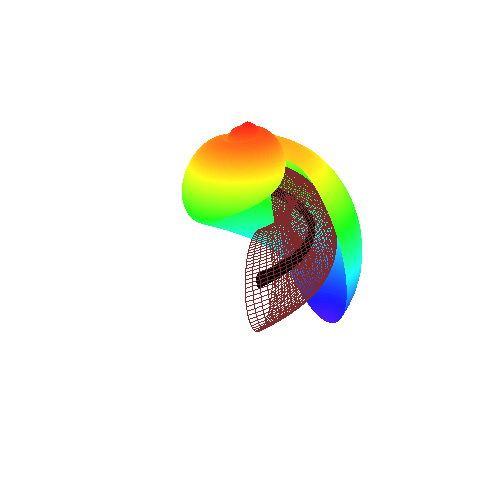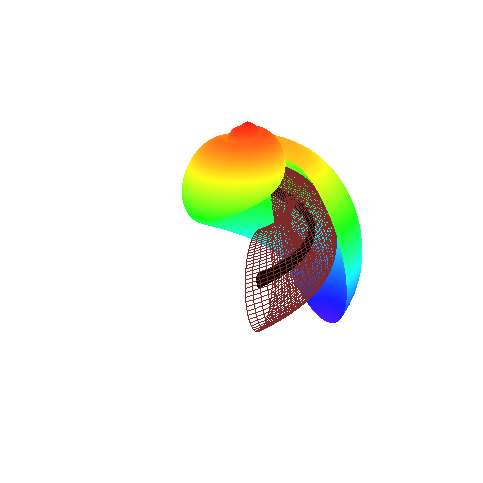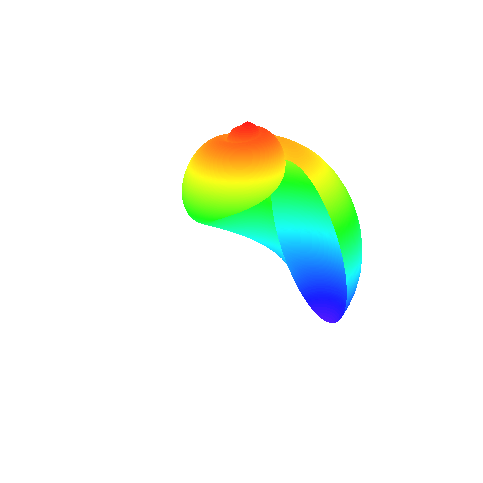
Lyria
![]()
| > | Ld:=[83.9,-19,45,1,-2,50,40,14,0,6,27,8,8]: theta:=[-4*Pi,4*Pi]: S:=[-51,9]: Grid:=[80,150]: |
| > | SeaShell(Ld,Grid,theta,S,Lyria,style=patchnogrid,scaling=constrained,orientation=[-39,66],lightmodel=light2,shading=xyz); |
![[Maple Plot]](images/Innhold45.gif)
Turritella
![]()
| > | Ld:=[88.9,4,55,1,-2,22.2,1.3,1.5,0,0,0,0,0]: theta:=[-30*Pi,4*Pi]: S:=[-267,39]: Grid:=[30,250]: |
| > | SeaShell(Ld,Grid,theta,S,Turritella,style=patchnogrid,scaling=constrained,orientation=[-83,89],lightmodel=light2,shading=xy); |
![[Maple Plot]](images/Innhold47.gif)
| > |
Oxystele
![]()
| > | Ld:=[84.9,7,-36,1,-2,47,40,19,0,6,27,8,0]: theta:=[-20*Pi,4*Pi]: S:=[-70,70]: Grid:=[40,350]: |
| > | SeaShell(Ld,Grid,theta,S,Oxystele,style=patchnogrid,scaling=constrained,orientation=[-26,91],lightmodel=light2,shading=xyz); |
![[Maple Plot]](images/Innhold49.gif)
| > |
Planorbis
![]()
| > | Ld:=[84,85,10,45,5,45,20,30,0,0,0,0,0]: theta:=[-1*Pi,4*Pi]: S:=[-150,130]: Grid:=[50,150]: |
| > | SeaShell(Ld,Grid,theta,S,Planorbis,style=patchnogrid,scaling=constrained,orientation=[-94,65],lightmodel=light3,shading=xy); |
![[Maple Plot]](images/Innhold51.gif)
Ammonite
![]()
| > | Ld:=[83,90,1,1,1,2.5,1.0,0.9,10,100,20,15,0.5]: theta:=[-Pi,4*Pi]: S:=[-170,170]: Grid:=[40,160]: |
| > | SeaShell(Ld,Grid,theta,S,Ammonite,style=patchnogrid,scaling=constrained,orientation=[-90,62],lightmodel=light4,shading=xy); |
![[Maple Plot]](images/Innhold53.gif)
Conus
![]()
| > | Ld:=[87,7,78,0,0,7,4.3,1.0,0,0,0,0,0]: theta:=[-12*Pi,4*Pi]: S:=[-180,2]: Grid:=[60,280]: |
| > | SeaShell(Ld,Grid,theta,S,Conus,style=patchnogrid,scaling=constrained,orientation=[-81,94],lightmodel=light2,shading=xy); |
![[Maple Plot]](images/Innhold55.gif)
Helcion
![]()
| > | Ld:=[18,90,0,0,-40,450,400,310,0,0,0,0,0]: theta:=[-0,4*Pi]: S:=[-180,180]: Grid:=[60,100]: |
| > | SeaShell(Ld,Grid,theta,S,Helcion,style=patch,scaling=constrained,orientation=[121,103],color=eggshell); |
![[Maple Plot]](images/Innhold57.gif)
Nautilus
![]()
| > | Ld:=[80,90,0,0,0,2,2,1.5,0,0,0,0,0]: theta:=[Pi,4*Pi]: S:=[-163,163]: Grid:=[30,60]: |
| > | SeaShell(Ld,Grid,theta,S,Nautilus,style=patchnogrid,scaling=constrained,orientation=[-79,54],lightmodel=light2,shading=xyz); |
![[Maple Plot]](images/Innhold59.gif)
Codakia
![]()
| > | Ld:=[37,90,0,1,1,10500,10000,10500,0,0,0,0,0]: |
| > | theta:=[-Pi,4*Pi]: S:=[-180,180]: Grid:=[100,100]: |
| > | SeaShell(Ld,Grid,theta,S,Codakia,style=patch,scaling=constrained,orientation=[-122,-58],color=gainsboro); |
![[Maple Plot]](images/Innhold61.gif)
Ukjent
![]()
| > | Ld:=[83,90,1,1,1,2.5,1,0.9,Pi/18,5*Pi/9,Pi/9,15,1/2]: theta:=[-Pi,3*Pi]: S:=[-170,170]: Grid:=[150,250]: |
| > | SeaShell(Ld,Grid,theta,S,Utvekster,style=patchnogrid,scaling=constrained,orientation=[-90,15],lightmodel=light2,shading=xy); |
![[Maple Plot]](images/Innhold63.gif)
Struthiolaria
![]()
| > | Ld:=[86.9,13,40,10,30,5,1.8,1.6,-15,5,5,16,1/2]: |
| > | theta:=[-20*Pi,4*Pi]: S:=[-168,24]: Grid:=[50,350]: |
| > | SeaShell(Ld,Grid,theta,S,Struthiolaria,style=patchnogrid,scaling=constrained,orientation=[-58,82],lightmodel=light2,shading=xy); |
![[Maple Plot]](images/Innhold65.gif)
Forvitring av et skjell
![]()
| > | Ld:=[84.2,20,-55,0,0,20,7.5,5,0,6,27,8,0]: |
| > | theta:=[-20*Pi,4*Pi]: S:=u->[-180,-25*u]: Grid:=[50,350]: |
| > | p:=u->SeaShell(Ld,Grid,theta,S(u),Struthiolaria,style=patch,scaling=constrained,orientation=[-85,50],color=light_tan): |
| > | display(seq(p(u),u=-6..1),insequence=true); |
![[Maple Plot]](images/Innhold67.gif)
Sluttproduktet uten gridlinjer
| > | SeaShell(Ld,Grid,theta,S(1),Struthiolaria,style=patchnogrid,scaling=constrained,orientation=[73,77],lightmodel=light4,color=light_tan); |
![[Maple Plot]](images/Innhold68.gif)
Smultring
| > | Ld:=i->[90,90,0,0,0,25,6+i/80,(i/80)^2,0,0,0,0,0]: theta:=[-4*Pi,4*Pi]: S:=[-270,90]: Grid:=[20,40]: |
| > | s1:=i->SeaShell(Ld(i),Grid,theta,S,Natalina,style=wireframe,scaling=constrained,orientation=[-68,54],color=coral): |
| > | display(seq(s1(i),i=90..240),insequence=true,scaling=constrained,orientation=[-68,54]); |
![[Maple Plot]](images/Innhold69.gif)
![[Maple Plot]](images/Innhold70.gif)
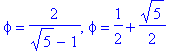
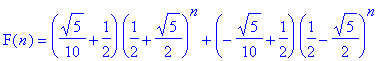
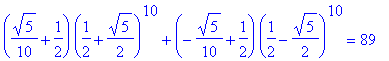
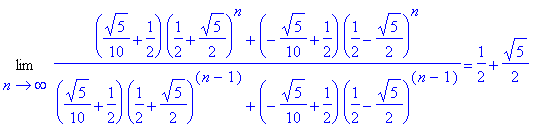

![matrix([[1, 0, 0, 0, 0, 0, 0, 0, 0, 0], [1, 1, 0, 0, 0, 0, 0, 0, 0, 0], [1, 2, 1, 0, 0, 0, 0, 0, 0, 0], [1, 3, 3, 1, 0, 0, 0, 0, 0, 0], [1, 4, 6, 4, 1, 0, 0, 0, 0, 0], [1, 5, 10, 10, 5, 1, 0, 0, 0, 0],...](images/Innhold89.gif)
![[Maple Plot]](images/Innhold90.gif)
![[Maple Plot]](images/Innhold91.gif)
![[Maple Plot]](images/Innhold92.gif)
![[Maple Plot]](images/Innhold95.gif)
![[Maple Plot]](images/Innhold96.gif)
![[Maple Plot]](images/Innhold97.gif)
![[Maple Plot]](images/Innhold98.gif)
![f[n+1]*f[n-1]-f[n]^2 = (-1)^n](images/Innhold99.gif)
![[Maple Plot]](images/Innhold101.gif)
![[Maple Plot]](images/Innhold102.gif)
![[Maple Plot]](images/Innhold103.gif)
![[Maple Plot]](images/Innhold104.gif)
![[Maple Plot]](images/Innhold105.gif)
![[Maple Plot]](images/Innhold106.gif)
![[Maple Plot]](images/Innhold107.gif)
![[Maple Plot]](images/Innhold108.gif)
![[Maple Plot]](images/Innhold109.gif)
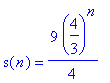
![[Maple Plot]](images/Innhold113.gif)
![[Maple Plot]](images/Innhold114.gif)
![[Maple Plot]](images/Innhold115.gif)
![[Maple Plot]](images/Innhold116.gif)
![[Maple Plot]](images/Innhold117.gif)
![[Maple Plot]](images/Innhold118.gif)
![[Maple Plot]](images/Innhold119.gif)
![[Maple Plot]](images/Innhold123.gif)
![[Maple Plot]](images/Innhold124.gif)
![[Maple Plot]](images/Innhold125.gif)
![[Maple Plot]](images/Innhold126.gif)
![[Maple Plot]](images/Innhold130.gif)
![[Maple OLE 2.0 Object]](images/Innhold134.gif)
![[Maple OLE 2.0 Object]](images/Innhold138.gif)
![[Maple OLE 2.0 Object]](images/Innhold142.gif)
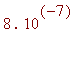 .
.
![[Maple Bitmap]](images/Innhold147.gif)
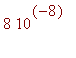 .
.
![[Maple Bitmap]](images/Innhold152.gif)
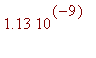 .
.
![[Maple Bitmap]](images/Innhold157.gif)
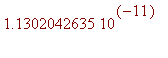 .
.
![[Maple Bitmap]](images/Innhold162.gif)
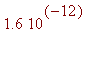 .
.
![[Maple Bitmap]](images/Innhold167.gif)
![[Maple OLE 2.0 Object]](images/Innhold168.gif)
![[Maple OLE 2.0 Object]](images/Innhold169.gif)
![[Maple OLE 2.0 Object]](images/Innhold170.gif)
![[Maple OLE 2.0 Object]](images/Innhold171.gif)
![[Maple Plot]](images/Innhold172.gif)
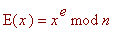 .
.