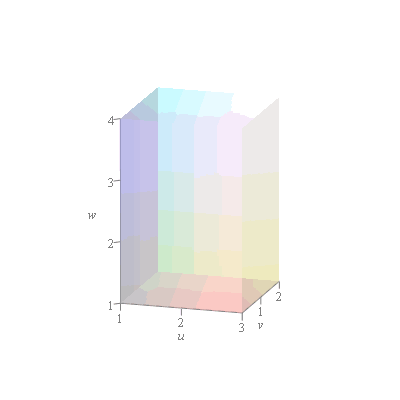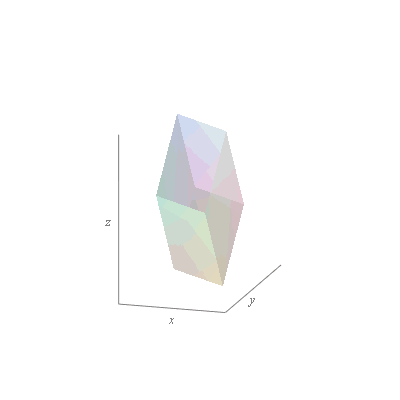Change of Variables in Multiple Integrals
Carl Gustav Jacob Jacobi was one of Germany's most distinguished mathematicians during the first half of the nineteenth century. He worked and studied the functional determinant now called the Jacobian. Jacobi was not the first to study the functional determinant which now bears his name. But his work with functional determinants is what secured his place in history. Jacobi wrote a long memoir called De determinantibus functionalibus in 1841 devoted to the Jacobian. This determinant is in many ways the multivariable analogue to the differential of a single variable. |
Carl Gustav Jacob Jacobi 1804-1851
was born in Potsdam, Prussia (now Germany) and died in Berlin, Germany |
We have already seen that for functions of one variable the chain rule
![]()
at once gives the rule for change of a variable in a definite integral
![]()
![]()
![]()
![]()
There is a formula analogous to this for double and triple integrals.
Change of Variables for Double Integrals
Let ![]() be a continuous function on a region
be a continuous function on a region ![]() in the
in the ![]() -plane, and let the transformation
-plane, and let the transformation ![]() maps the region
maps the region ![]() in the
in the ![]() -plane into the region
-plane into the region ![]() . Then
. Then
![]()
![]()
![]()
![]()
where ![]() is the Jacobian and
is the Jacobian and ![]() represents either
represents either ![]() or
or ![]()
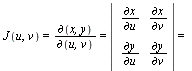
![]()
![]()
![]()
![]()
Change of Variables for Double Integrals
The change of variables formula for triple integrals is similar to the one given above for double integrals.
Change of Variables for Triple Integrals
Let ![]() be a continuous function on a region
be a continuous function on a region ![]() in the
in the ![]() -space, and let the transformation
-space, and let the transformation ![]() maps the region
maps the region ![]() in the
in the ![]() -space into the region
-space into the region ![]() . Then
. Then
![]()
![]()
![]()
![]()
where ![]() is the Jacobian and
is the Jacobian and ![]() the region i
the region i ![]() -space.
-space.

Change of Variables for Double Integrals
If ![]() or
or ![]() is a one-to-one transformation, then
is a one-to-one transformation, then ![]() or
or ![]() it can be shown that
it can be shown that
![]() 1,
1, ![]() 1
1
The following commands in the calcplot package plot images of regions under arbitrary coordinate transformations. With these commands we can check whether the description of a new region under a change of coordinates is correct.
-
regionplot2d
(
![v = h(u) .. k(u), u = u[1] .. u[2], [x(u, v), y(u, v)]](images/Some Pages_758.gif) ) plots the image of a region in the
) plots the image of a region in the  -plane of the form
-plane of the form 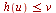
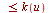 ,
, ![`<=`(u[1], u)](images/Some Pages_762.gif)
 under a coordinate transformation into
under a coordinate transformation into 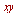 -plane given by the list
-plane given by the list 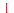
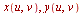
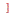 . The variable order is the same as if the
int
procedure were invoked for a
double integral
over the region
. The variable order is the same as if the
int
procedure were invoked for a
double integral
over the region
-
regionplot3d
(
![w = h(u, v) .. k(u, v), v = p(u) .. q(u), u = u[1] .. u[2], [x(u, v, w), y(u, v, w), z(u, v, w)]](images/Some Pages_768.gif) ) plots the image of a three-dimensional region in
) plots the image of a three-dimensional region in 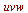 -space of the type
-space of the type 
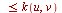 ,
, 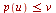
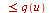 ,
, 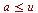
 ,
, ![`<=`(u[1], u)](images/Some Pages_776.gif)
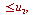 under a coordinate transformation into
under a coordinate transformation into 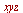 -space given by the list
-space given by the list 
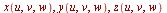
 . The variable order is the same as if the
int
procedure were invoked for a
triple integral
over the region.
. The variable order is the same as if the
int
procedure were invoked for a
triple integral
over the region.
In the
linalg
package
-
jacobian
(
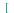 x
x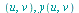 ...
...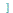 ,
, 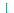 u,v,...
u,v,...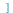 ) computes the Jacobian matrix of the vector or list
) computes the Jacobian matrix of the vector or list ![[x(u, v), y(u, v) .. ()]](images/Some Pages_787.gif) with respect to
with respect to 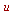 , v, ...
, v, ...
-
det
(jacobian)(
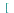 x(
x(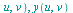 , ...
, ... ,
, u,v,...
u,v,... ) computes the determinant of the Jacobian matrix
) computes the determinant of the Jacobian matrix
-
Jacobian
(
 x(
x(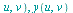 , ...
, ...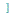 ,
,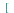 u,v,...
u,v,...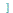 ,'determinant') computes the Jacobian matrix and the determinant
,'determinant') computes the Jacobian matrix and the determinant
Example 1
Find the region ![]() in the
in the ![]() -plane corresponding to the region
-plane corresponding to the region ![]() in the
in the ![]() -plane where
-plane where
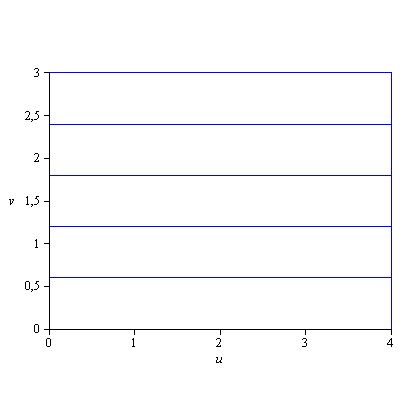
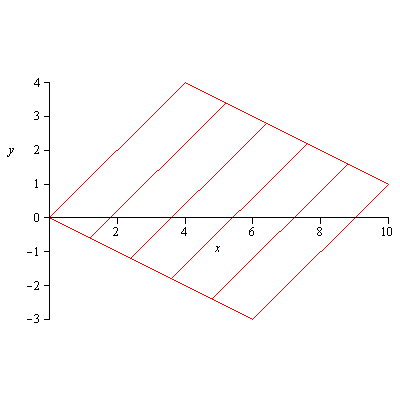
a) ![]()
![]() and
and ![]()
![]() under the change of variables
under the change of variables ![]() ,
, ![]() .
.
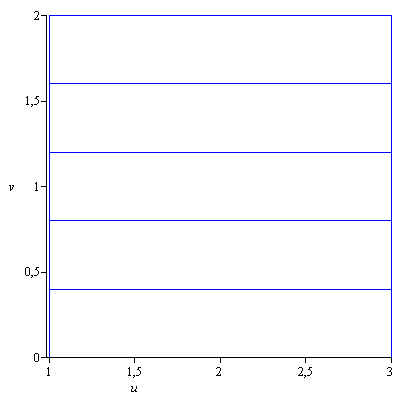
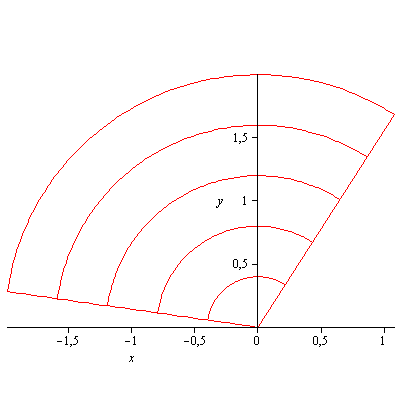
b) ![]()
![]() and
and ![]()
![]() under the change of variables
under the change of variables ![]() ,
, ![]() .
.
Find the region ![]() in the
in the ![]() -plane corresponding to the region
-plane corresponding to the region ![]() in the
in the ![]() -plane where
-plane where
c) ![]()
![]() ,
, ![]()
![]() , and
, and ![]()
![]() under the change of variables
under the change of variables ![]() ,
, ![]() .
.
| > | restart: MathMaple:-ini(): |
Solution
a)
|
|
b)
|
|
c)
|
|